Part of series software development | 2022-05-17

Retry Strategies

With the development of microservices, software as a service and cloud nowadays, network communication between components or services is the most important part of software development. But more network communications, we faced more network problems while developing the system.

Retry is one of the solutions to handle these problems. If the system got fails action, the system can do it again. There is the main idea of any retry strategy.

Let’s take a look at common retry strategies and their benefits when applying them.

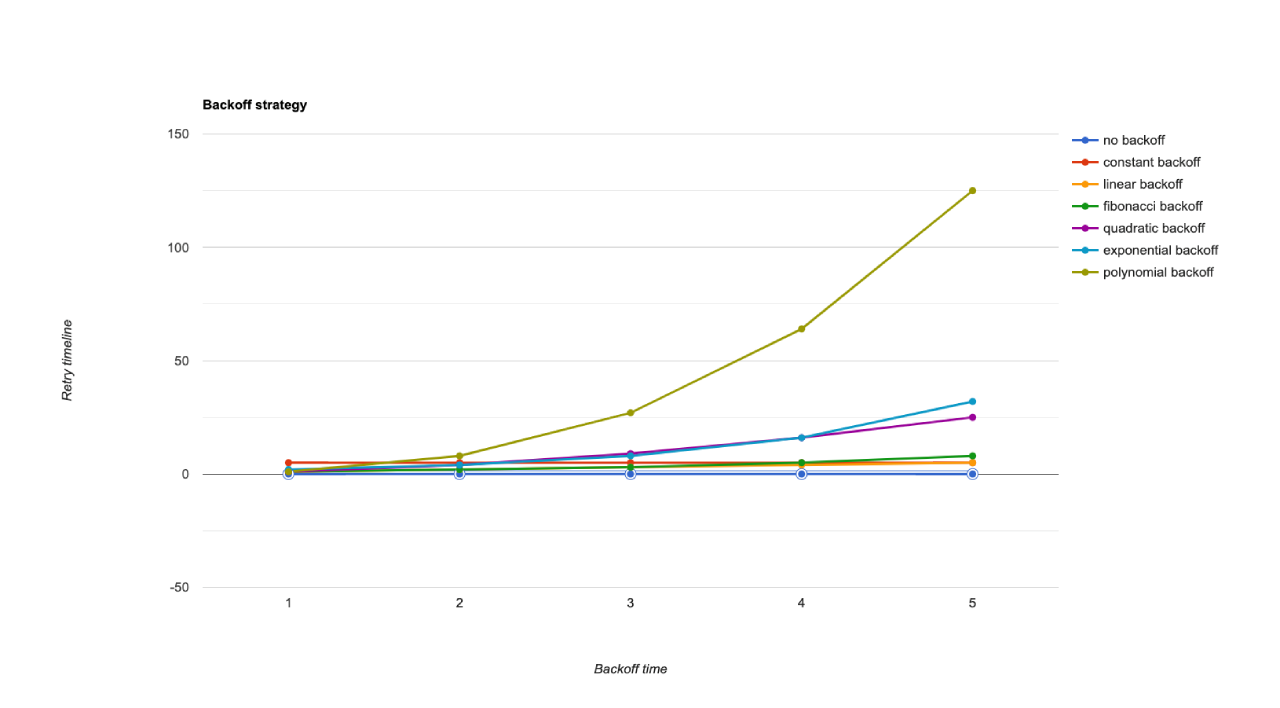
No Backoff

No backoff retry’s a super bare way to do retry strategy. It does the retry action immediately after failed action and has no waiting duration between retry actions if they fail.

duration(t) = 0

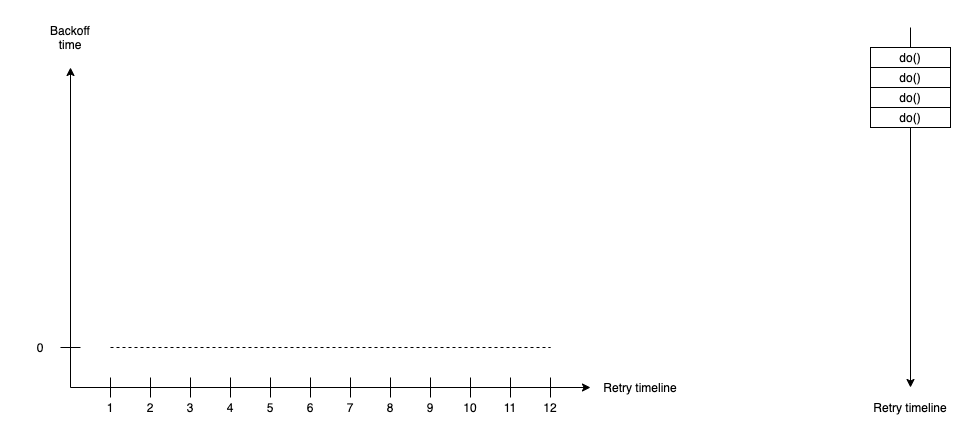
No backoff

No backoff retry strategy is also treated as bad practice because they make the system over-working by doing the retry actions extremely. It makes both caller and callee take resources when caller can’t handle process during that time.

The no backoff retry should be used in special cases where you are aware of what you are doing. If you are not sure, let to use one of the next strategies, that save your system better.

Constant Backoff

The most common way to implement the retry strategy. Constant backoff retry adds a fixed waiting duration after the first failure and between retry actions.

duration(t) = <constant value>

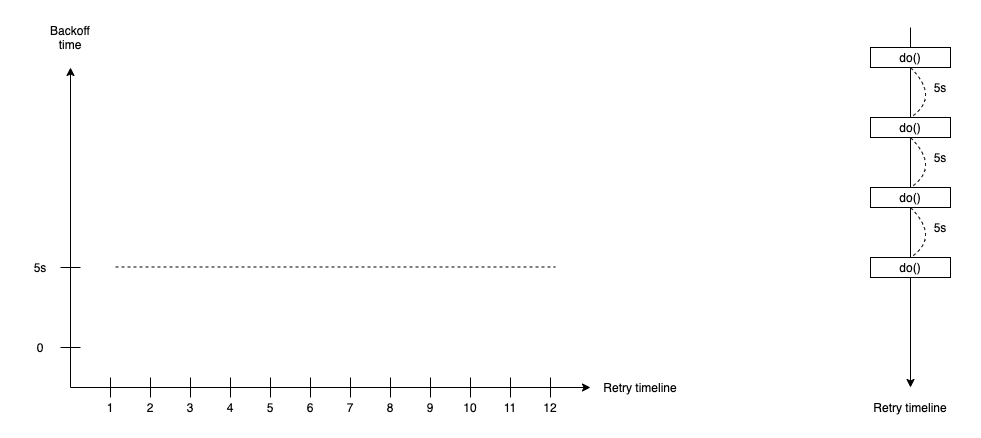
Constant backoff

The constant backoff retry gives callee time to breathe and recover if it failed. It provides more chances for the retry successful next time. The constant backoff works well in most situations when many concurrent retry action is small and the failed problem is fixed in a short time.

When the number of retry actions matters, especially network problems with many callers; or the system takes a long time to recover; the fixed waiting duration of constant backoff retry doesn’t give the best result. The stress is accumulated and makes the system longer to recover.

A term is if the system can’t recover after (x) duration, then it doesn’t have any proof about the system is back after the same (x) duration. So it should increase the next waiting time when we have more chances for recovering the system.

To handle it, they suggest the next solution.

Linear Backoff

The linear backoff retry strategy supports the waiting duration after the first failure and increases the waiting duration of the next retries. It increases constantly delta x from the previous waiting time with the formula:

duration(t) = duration(t-1) + x

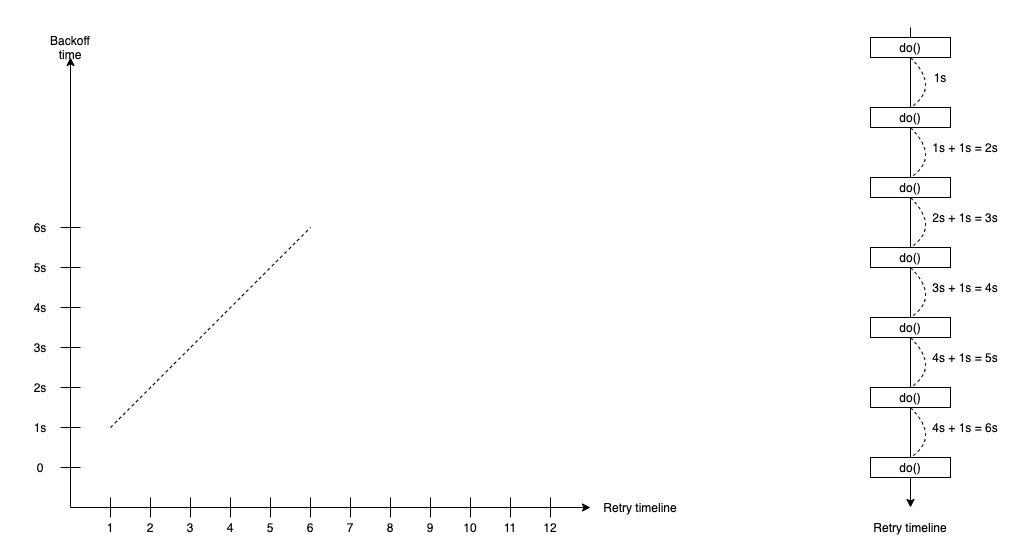
Linear backoff

In the linear backoff retry strategy, we define constantly delta x and first waiting duration(0).

Fibonacci Backoff

The Fibonacci backoff retry strategy supports the waiting duration that calculates by using the Fibonacci sequence with the formula:

duration(t) = duration(t-1) + duration(t-2)

In the Fibonacci backoff retry strategy, we define the first and second waiting duration(0) and duration(1).

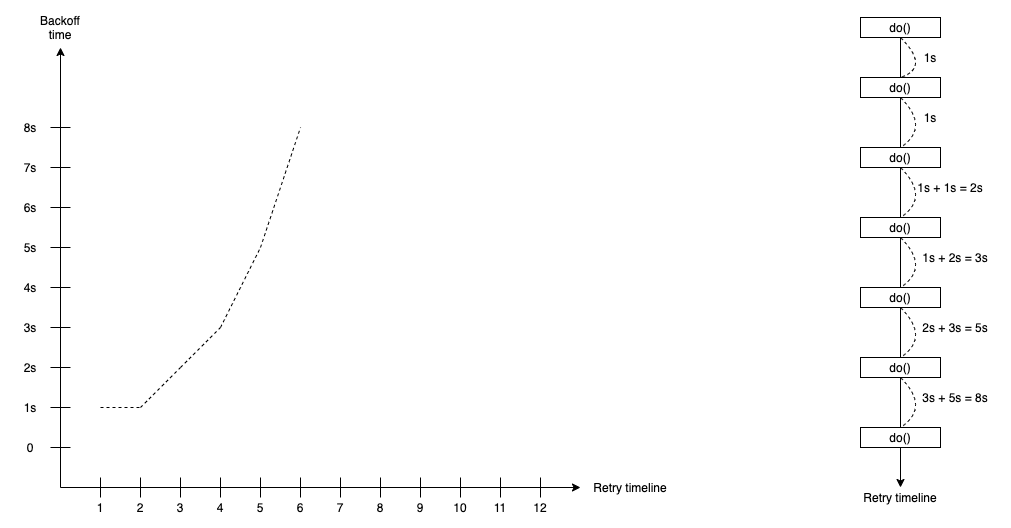
Fibonacci backoff

Quadratic Backoff

The quadratic backoff retry strategy supports the waiting duration that calculates by following the quadratic curve with the formula:

duration(t) = attempt ^ 2 * base-time

In the quadratic backoff retry strategy, we define the base-time duration, such as 1s or 100ms. The attempt is time we do retry.

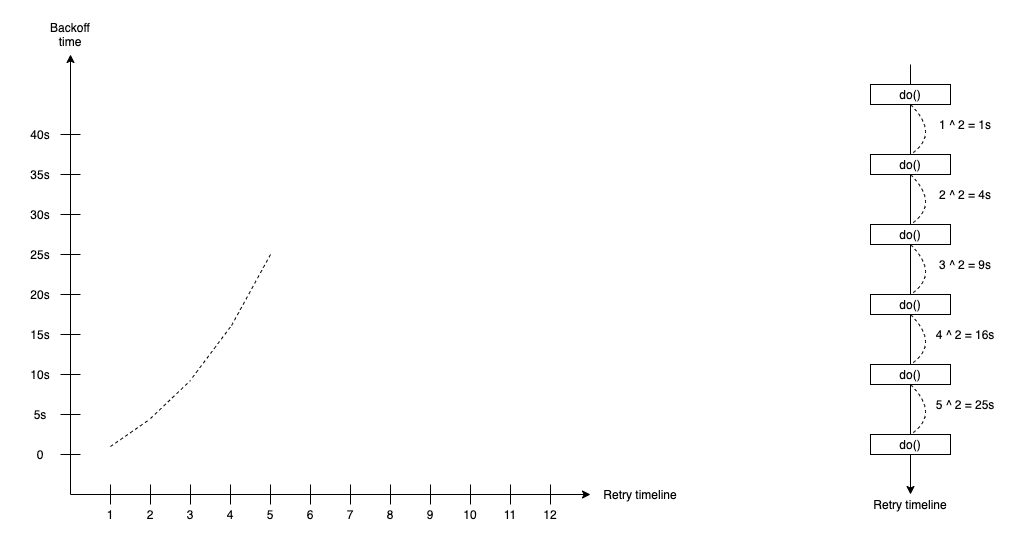
Quadratic backoff

Exponential Backoff

The exponential backoff retry strategy supports the waiting duration that calculates by following the exponential curve with the formula:

duration(t) = 2 ^ attempt * base-time

In the exponential backoff retry strategy, we define the base-time duration, such as 1s or 100ms. The attempt is time we do retry.

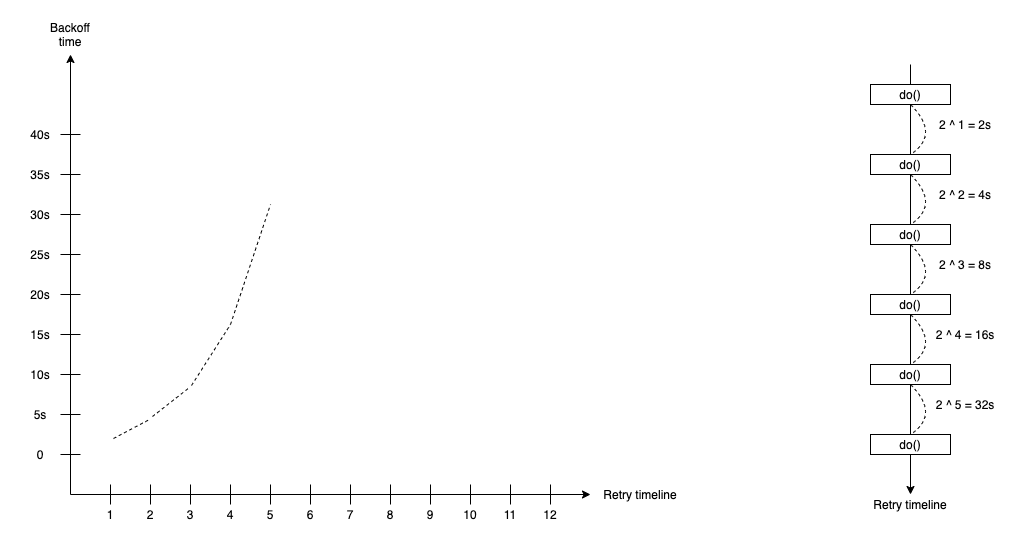
Exponential backoff

Polynomial Backoff

The Polynomial backoff retry strategy supports the waiting duration that calculates by following the formula:

duration(t) = attempt ^ degree * base-time

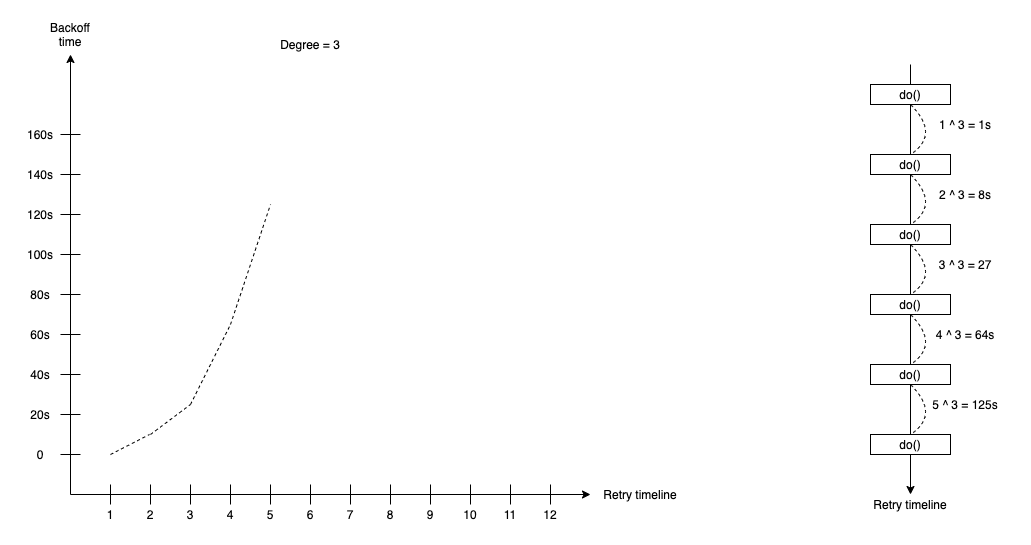
Polynomial backoff

In the Polynomial backoff retry strategy, we define the degree and base-time duration, such as 1s or 100ms. With polynomial backoff, we can define degree number input, so quadratics is a special case of polynomial backoff with the fixed degree is 2. The attempt is time we do retry.

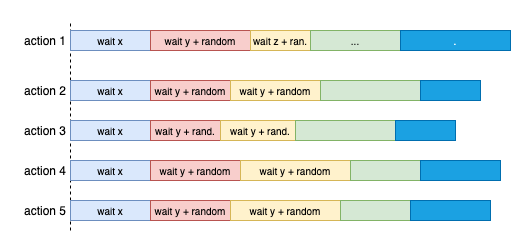
Jitter

Suppose we have multiple retry callers do an action or send requests that collide and fail. They all decide to retry with a backoff strategy. They will all retry at the same time, which leads to colliding again.

Jitter is a technique to solve that problem. It adds or removes different random waiting durations to back off time. So each next retry will happen at a different time and help to avoid several calls next time.

Jitter backoff

External references:

Retry Strategies and Patterns